A Marvelous Message Moving Marble Machine Ch. 1

Talking computers

What does it mean when we say we want two computers to talk to each other? At the most basic level, computer A should be capable of sending a message to computer B, and computer B should be capable of responding with a message of its own.

What’s a message, you might ask? For our purposes a message is a grouping of related information. Information can be broken up into different units. We’ll start with the smallest unit, the bit. One bit is the amount of information you need to answer a yes or no question. Therefore, the smallest message a computer can send is a simple yes or no.

Marvelous marbles

Let’s build an imaginary device that allows us to pass the simplest possible message. Imagine a small length of clear plastic tubing just big enough to pass a marble through. The tube is angled to allow a marble to roll from one end to the other, with an opening to drop in the marble at one end. We’ll call the person sending the marble Alice.

At the other end of the tube, there’s another opening for the marble to exit. A person can stand at the exit and observe the marble rolling out. We’ll call the person on the exit side Bob.

Bob can yell out a question with a yes or no answer to Alice, and Alice can respond by either dropping in a marble or not. If Alice sends a marble down the tube, when Bob sees it, he knows the answer to his question is yes. If he doesn’t see a marble, he knows the answer is no. A marble means yes. No marble means no.

There’s a problem here, however. What happens when Alice and Bob are too far away to hear each other? Alice and Bob need to agree on what question the marbles are answering ahead of time.

Imagine this scenario. Alice and Bob are in separate adjacent classrooms. Each classroom has a clock, and Bob and Alice want to keep the clocks synchronized. Theres a long tube that runs through a hole in the wall between two classrooms. In one classroom, Alice will drop a marble in the tube at the top of each hour according to her clock. In the next classroom, Bob will watch the tube. When a marble rolls out, Bob will record a “Yes”, and reset his clock back or forward to the nearest hour. As long as the the clocks aren’t running much too fast or slow, and Bob and Alice are paying attention, they’ll never get too far out of sync.

This works because Alice and Bob agreed ahead of time that the question the marble is answering is “Is it currently the top of the hour?”. They already know the question, so there is no need for Bob to try to yell the question to Alice.

Green means go

Can you spot any problems with this setup?

One problem is that we can’t tell the difference between someone sending the message No and someone sending no message at all. What happens if Alice runs out of marbles, or the tube gets clogged up? Bob can’t tell the difference between a problem with the system and a No message.

There’s an easy solution for this. We’ll use 2 different colored marbles. Green for Yes and red for No.

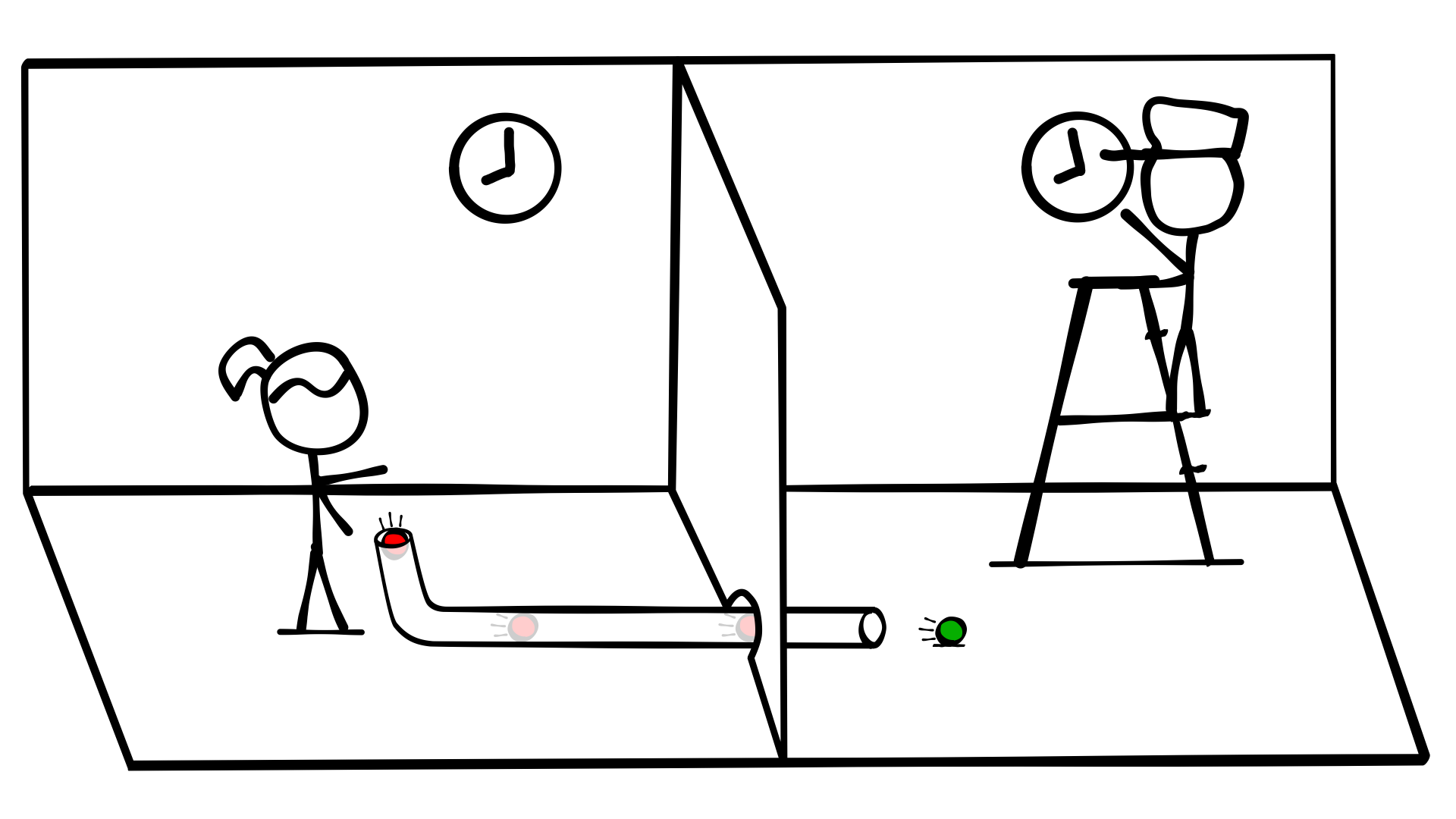
Now we can have Alice keep sending red marbles until the clock reaches the top of the hour. Then she sends a green one. If marbles stop coming through the tube all together Bob knows something is wrong.

With this system, we can send a stream of as many yeses and noes as we want. As long as the person receiving the messages knows what questions the messages are intended to answer, this system works well.

Marvelous maritime marbles

Imagine another scenario. Bob is steering a ship, and Alice is the lookout. Alice is up in the crows nest too far away for Bob to hear. If Alice sees something ahead, she needs to be able to warn Bob and tell him whether he should steer left or right to avoid it.

Luckily for Bob and Alice, they have one of our Marvelous Marble Machines. The exit is next to Bob, and the entry opening is with Alice in the crows nest, ready to relay marbles.

How can Alice send all the information that Bob needs? To start with, Alice can continue to send noes as long as she doesn’t see anything the ship will collide with. When she sees something, she sends a yes. After she sends a yes, she sends another message to tell Bob which direction to turn. If she sends a yes, Bob should turn right. If she sends a no, Bob should turn left. After the direction, she keeps sending more noes until she spots something else.

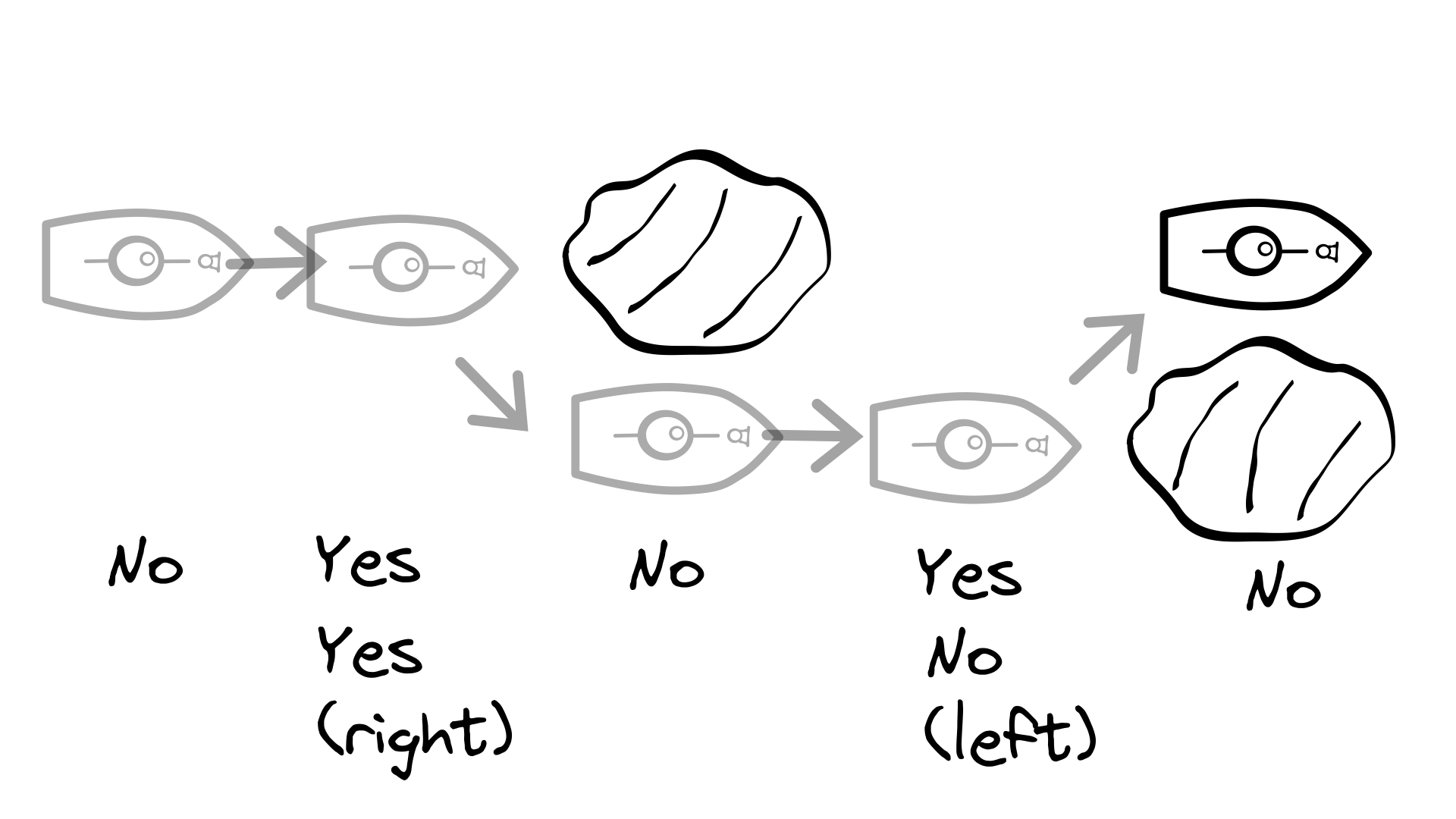
In the above image, Alice send the following marbles: Red, Green, Green, Red, Green, Red, Red–No, Yes, Yes, No, Yes, No, No. This translates to: nothing there, rock ahead, turn right, nothing there, rock ahead, turn left, nothing there.

Letters are better

But what happens when we want to send more complex messages? It turns out that we can send any arbitrary letter of the alphabet (and eventually long sequences of letters) using a variation of the same technique we just used to avoid obstacles.

First we take the 26 letters of the alphabet. We then add a few extra characters to the end of the list to make a total of 32 characters (32 makes the process a little more straightforward because 32 is a power of 2. That means each time you divide it in half both sides are always equal).

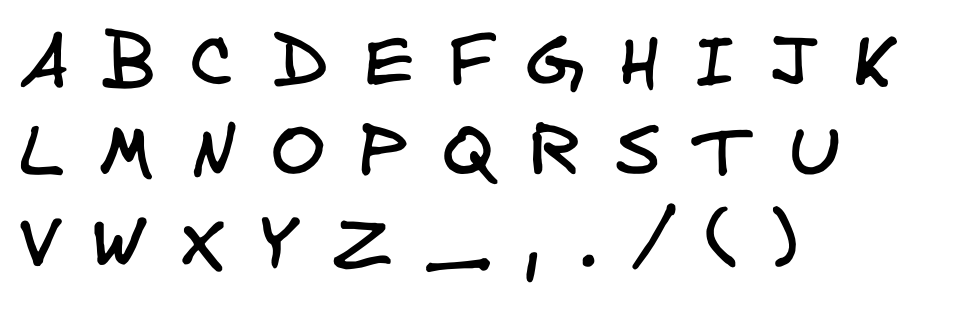
Now all we have to do is figure out which questions we need to send the answer to. The question doesn’t have to be yes or no - it only needs to have exactly 2 possible answers. Let’s pick a letter and then start asking questions until we figure out which letter we chose.

1. Cut the letters in half. Is our letter in the left or right group of letters? Right.
2. Cut them in half again. Is our letter in the left or right group? Left.
3. Again. Left or right? Left.
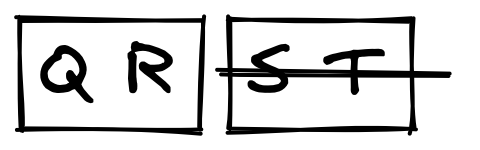
4. Again? Left.
5. Cut them in half once more. Left or right? Right. Now we're down to one letter, and we have our answer. The letter R.

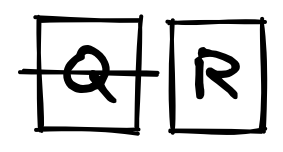
32 can be divided in half exactly 5 times (2^5 = 32), so it takes 5 questions to identify a letter. Therefore, by sending lefts and rights in groups of 5, we can send any arbitrary letters we want.

Let’s try another one.

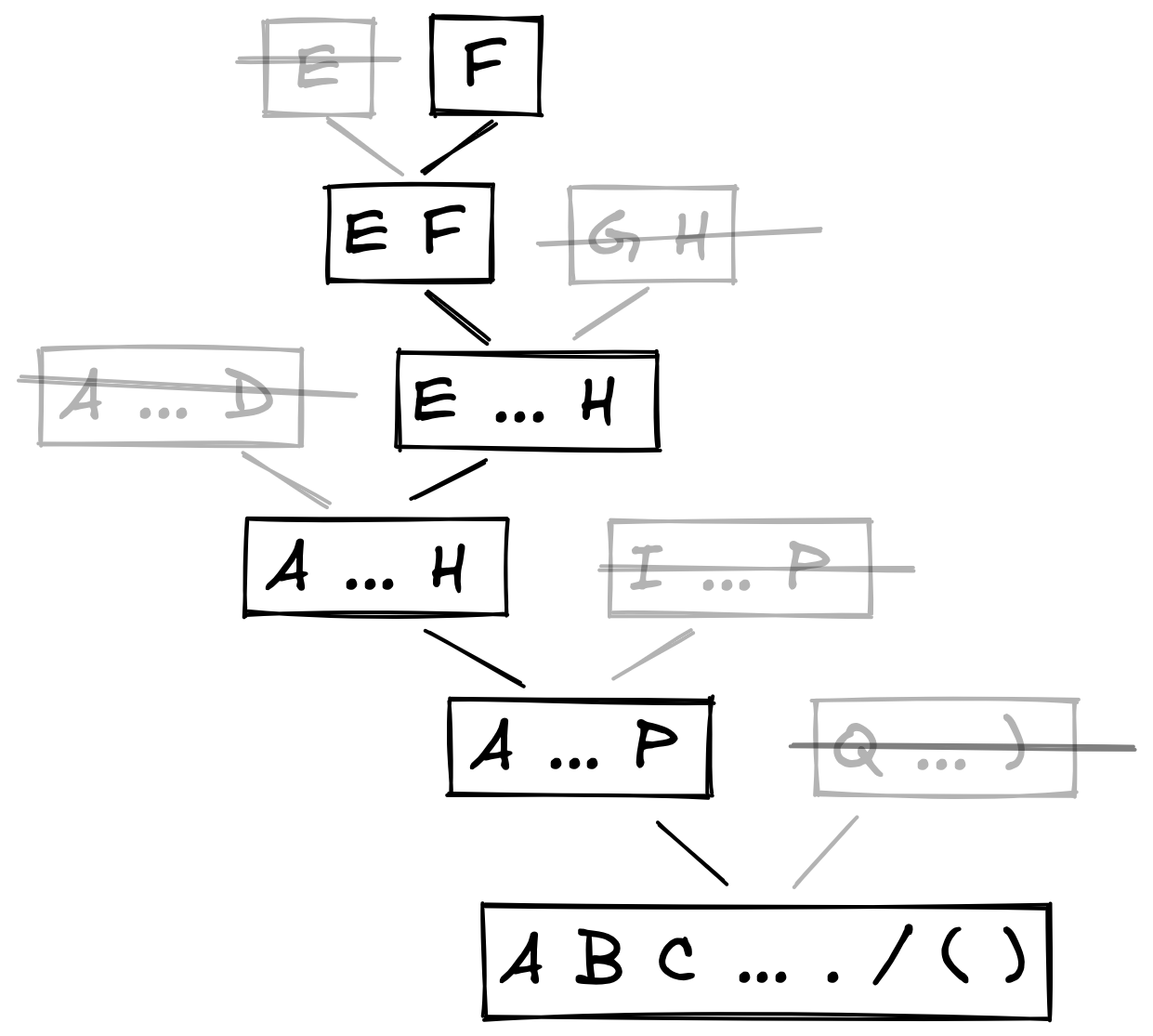
Left-Left-Right-Left-Right leads us to the letter F.

Binary is better?

We’ve seen that the letter F can be represented as the sequence Left-Left-Right-Left-Right. We can find a more convenient way to represent this sequence. Instead of Left and Right we can use 0 and 1. 0 for Left and 1 for Right. So Left Left Right Left Right becomes 00101.

As it happens, 00101 is also binary for the number 5. If you start counting at 0 (A = 0, B = 1, C = 2, and so on), then F is also number 5.

The binary number system is similar to the decimal number system except that it’s based on powers of 2 instead of powers of 10. In the decimal system we have the ones place, the tens place, the hundreds places and so on. In binary we have the 1s places, the 2s place, the 4s place, the 8s place, and we keep doubling each time.

Let’s take a look at the decimal system first. For most of us this is something we learned so long ago that we no longer think about exactly how it works. But it’s worth examining, so that we can see the parallels in the binary system.

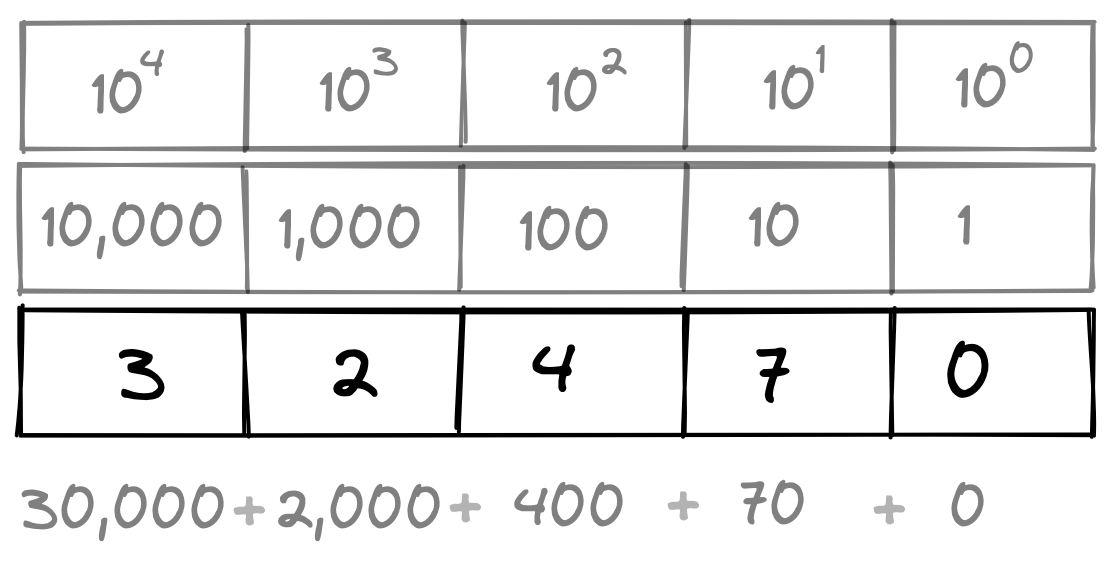
We can see that each place increases by 10 times as we move from right to left, and the number in each position tells us how many of each place to add to the total. In this case we add 0 ones, 7 tens, 4 hundreds, 2 thousands, and 3 ten-thousands to get 32,470.

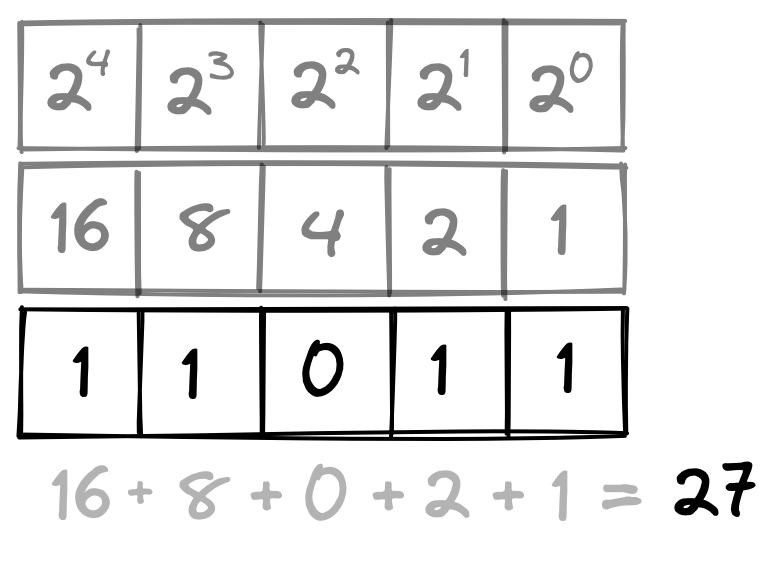
The binary number system works in much the same way, except that instead of each position increasing by 10 as we move from left to right, each position doubles. Also, instead of each place having 10 possible values (0 through 9), each place only has 2 possible values (0 and 1).

A 0 tells us that nothing should be added to the total for that position, and a 1 tells us that 1 of the place value should be added. In the example above, 11011, we add 1 of the ones place, 1 of twos place, 0 of the 4s place, 1 of the eights place and 1 of the sixteens place for a total value of 27. Each digit in the binary number system is called a bit (remember, a bit is also the amount of data needed to answer a yes or no question).

Circling back to the alphabet, we can see that since every letter in our alphabet can be represented by a series of 5 left or right directions, and since a left or right can be represented as a 0 or 1, every letter in our alphabet can be represented by a sequence of 5 binary digits. 5 bits. A is 00000, B is 00001, F is 00101 and so on. If you want to, you can take the time to work through cutting the alphabet in half and going to the left or the right each time you want to work out the letter. Or you can use this handy table.

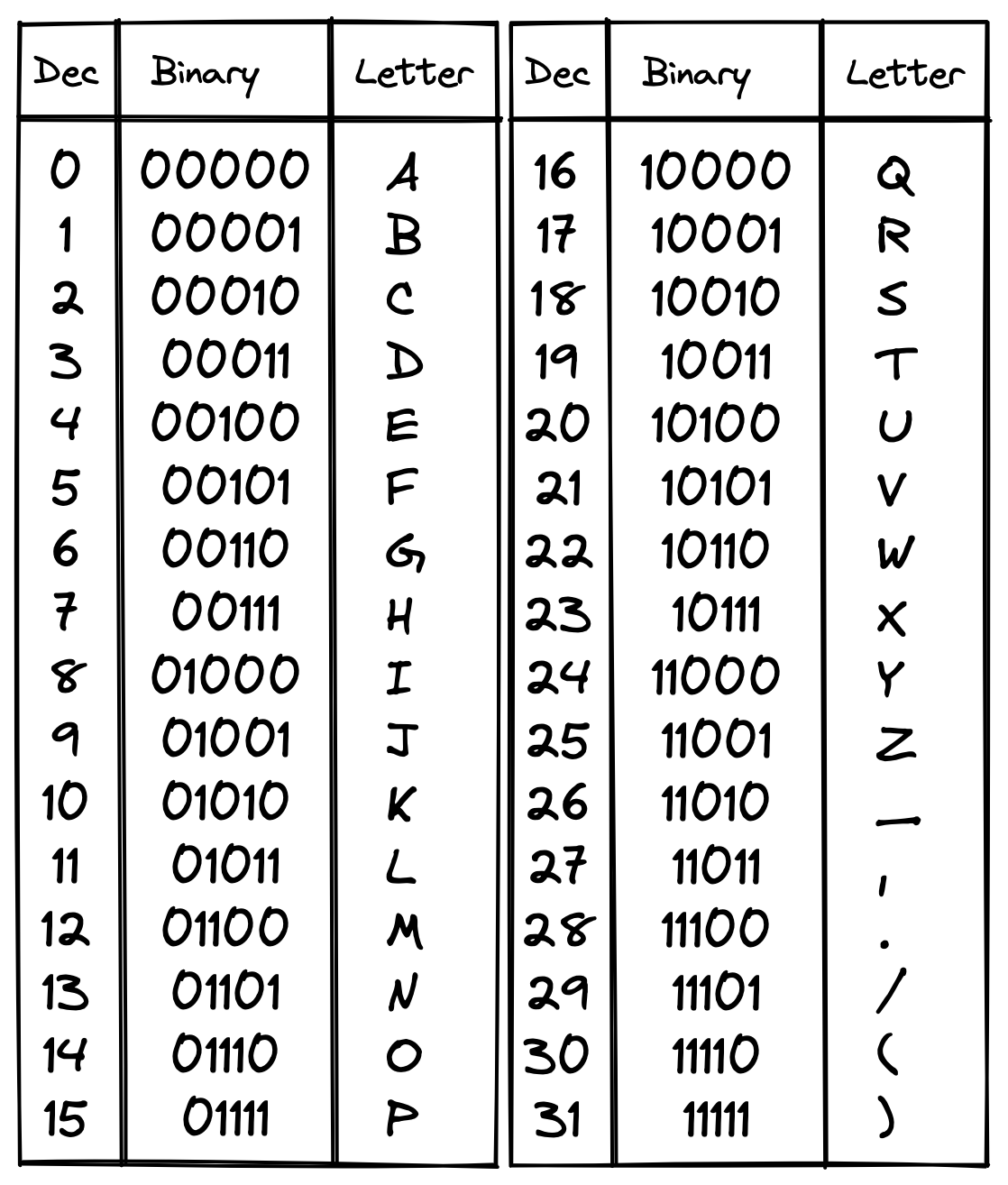
Messages in a bottle

Now how does Alice go about sending one of these letters over our marble tube device? Let’s use the same convention as before with the ship. A red marble is left or 0, and a green marble is right or 1. Instead of a ship, let’s put Alice and Bob back into two rooms, a bit like the rooms from the clock example.

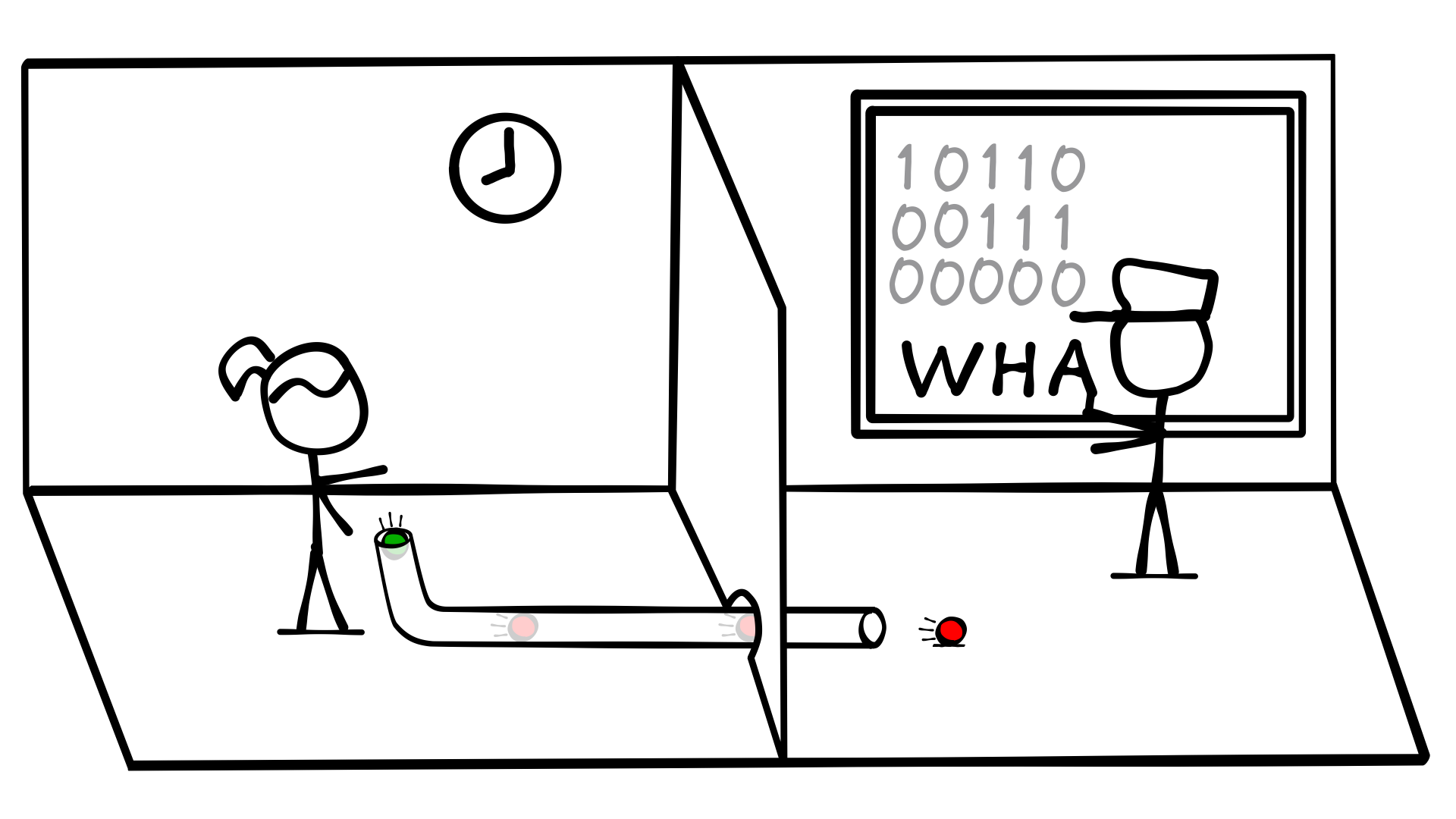
To send the letter W, Alice looks at the table and notes that the binary for W is 10110. Next she reads the sequence from left to right and sends one marble at a time. One marble for each bit. Green Red Green Green Red. 10110.

Then, on the other end of the tube, Bob writes down the sequence from left to right as it comes in. When Bob has 5 digits, he can use his copy of the table to write down the letter. Alice can keep doing this over and over to send an entire message.

Division of labor

Bob and Alice have a lot to do in this scenario. Alice has to break up the message into letters, lookup the binary code for each letter in the table, and then send a marble for each bit in the binary representation of the letter.

Bob has to monitor the marbles leaving the tube, decide whether they are green or red, remember that green is 1 and red is 0, write down each bit, group the bits into 5-bit sequences, and finally look up the binary number in the table to write down the correct letter.

What if we break down each person’s job into 3 parts. Instead of 2 rooms, we now have 2 buildings. Building A and building B. Each building has with 3 floors, and there are now 3 Bobs and 3 Alices, one on each floor.

A message starts with the Alice at the top of building A on the 3rd floor. Alice is given a message and she writes down each letter on the whiteboard. She writes down the first letter on a piece of paper and places it in a small elevator to send down to floor 2. Alice then writes down the next letter on another piece of paper and waits for floor 2 to send the elevator back up. When the elevator comes back, she knows that floor 2 is ready for another letter, so she sends down her second letter. This continues until she has sent each letter in the message.

Meanwhile, Alice on floor 2 sees the letter sent by floor 3 and looks up that letter in her copy of the binary to letter table. She copies down the sequence of bits on her whiteboard. Next, she writes the first bit on a piece of paper and sends it down the elevator to floor 1. She then waits for floor 1 to send the elevator back for the next bit. She repeats this until all the digits for the current letter have been sent down, and she sends the elevator back up to floor 3 for the next letter.

When Alice on floor 1 sees a bit arrive on the elevator from floor 2, she drops a marble in the tube to building B - a green marble for 1 and a red marble for 0. She then sends the elevator back up to floor 2 to indicate she is ready for another bit.

A similar process happens in building B but in reverse. Bob on floor 1 watches the marbles come out of the tube and writes down the correct bit (1 or 0). Then he writes down the bit and sends it up the elevator, where Bob from floor 2 copies the bit on a whiteboard and sends the elevator back down to floor 1. This repeats until the floor 2 Bob has written 5 bits. When he has 5 bits, he uses a copy of our table to look up the letter, and sends it up to Bob 3.

Bob 3 adds the letter to his whiteboard, then sends the elevator back down to floor 2. This continues until the message is complete on the floor 3 whiteboard.

The floors build on each other. As you move up the floors, the information on each floor gets assembled into something more complex. Marbles turn into bits, bits combine into letters, and letters combine into messages. If you move down floors, the reverse happens. At each floor we break down the information into smaller components. Messages are broken into letters. Letters are broken into bits, and bits are converted into marbles. This is common in software engineering. It’s called layered architecture and it’s one of the ideas the internet is built around. Each floor in our example is a layer in layered architecture.

What’s the advantage of this? Each layer only needs to know a little bit about the entire process, just enough to communicate with the layer below or above. Floor 1 only needs to know how to turn bits into marbles or vice versa. Floor 2 only needs to know how to look up letters in the table, so they don’t need to know about marbles at all. And floor 3 only needs to know how to add letters together or break them apart. This way, if we decide we need to replace one of the floors/layers, it’s much easier.

In our example, if we want to replace the marbles with something else, we only have to tell floor 1. Floors 2 and 3 can continue their work without any knowledge or extra training. Imagine that we want to send messages over longer distances, so we replace our tube with carrier pigeons. The marbles are too heavy for the pigeons to carry, so we use pieces of paper with RED and GREEN written on them instead.

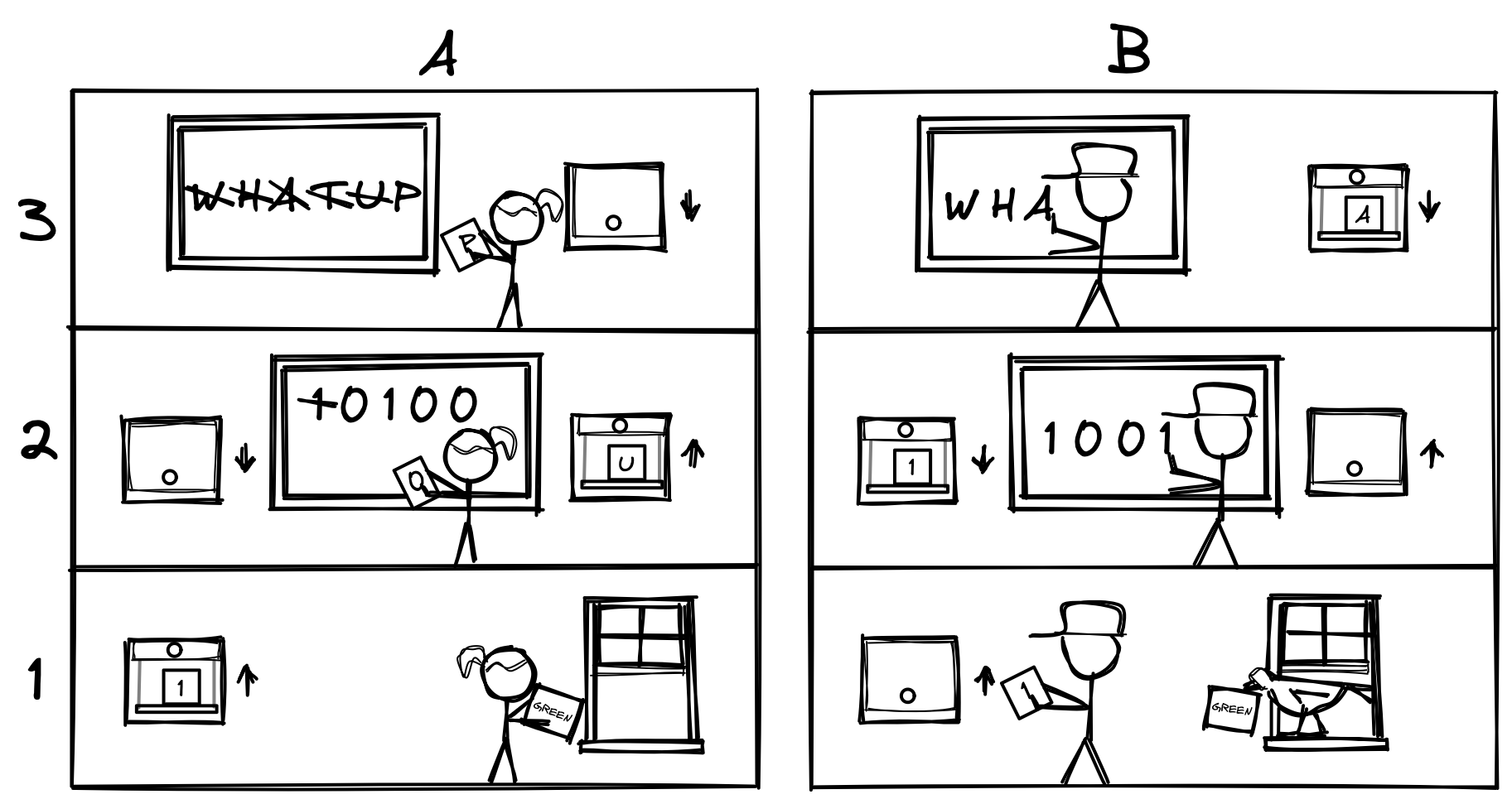
All we need to do is add a window, remove the marble tube, and teach Bob and Alice from floor 1 how to send carrier pigeons instead of marbles. As long as floor 1 keeps sending and receiving 1s and 0s to floor 2 just like before, the rest of the building won’t even know anything changed.

What’s next?

We started this chapter with a discussion about computers talking to each other. We’re finally ready to build an example of doing just that. We’ll start off the next chapter replacing components of our marble system with computer network equivalents.